Water Lilies, Water Lilies Everywhere

Note: This long-form essay I wrote last year goes more in-depth on the same topic.

I / Universes

Take a universe, one just like our own Universe, only much simpler. It's a square made up of 10,000 smaller squares, each of which can only be one of four colors at a time.

Like our Universe after the Big Bang, this little universe starts as a chaotic mess. This is what true randomness looks like:

Stare at it for a while. Replay the video a few times. What does it make you think of? How would you describe the phenomena occurring inside that square? What names would you give to the things you're observing?

Look at any specific pixel or region in that image. In some areas, it seems like groups of the same color stick together, but those alliances disappear in an instant, in the flicker of a single frame, never to be repeated. The color of each pixel is truly random, with no rhyme or reason, no explanation, nothing "causing" them to be a specific color instead of another. Anything could happen, and nothing is more likely to happen than anything else.

In a case like this, nothing you see can have a "name," be described, or talked about—all you can say is that there are pixels behaving randomly. Their behavior cannot be predicted.

This is what we call random: the unpredictable. If something is random, you can't predict what it will do next. The reverse is also true: if, despite your best efforts, something remains consistently unpredictable, you call it random.

Randomness and unpredictability are one and the same!

Now look at this other universe, which begins with exactly the same random arrangement of colors:

Do you notice anything? It's subtle, but there's something different going on. It still looks quite random, that's true, but isn't it a little less random than before? It's easier to notice if you compare the first frame,

with the last one,

It starts uniformly random, but by the end of the simulation, the frame appears somehow changed. During the simulation, the pixels seem to gradually form small clusters, thin filaments that you can distinguish from the messier regions around them. Although they wriggle around randomly and are rather unstable—melting away and reforming in unexpected ways—they linger longer than before and seem at least a bit more predictable. If you focus on a dark area for a moment and pause the video, you could guess that the area will continue being dark half a second later, even if its shape will have changed. Your prediction would be right more often than not.

What changed from the previous video? I only introduced a small twist: each pixel's color is partially affected by the colors it had around in the previous frame. If most of its eight pixel-neighbors were terracotta-colored at the previous step, for example, a pixel will turn terracotta next with a 60% chance. It still has a 40% probability of not turning terracotta, though, which is why the effects are still mostly random.

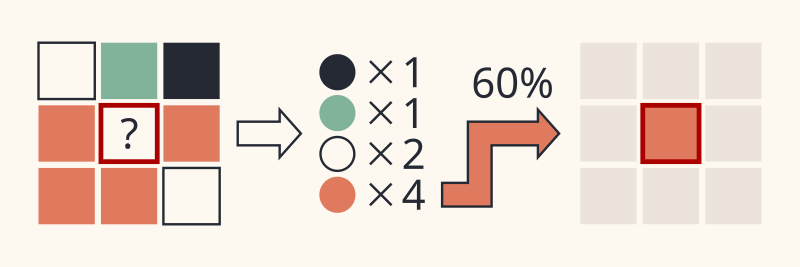
The effect of reducing randomness was the emergence of patterns. There you go! Even though these are still rather anonymous and elusive, we can finally use a noun to indicate the stuff that's going on in the frame—a luxury we didn't have in the fully-random universe.

That's not all: we can finally talk about what's happening. We can describe the behavior with something other than "it just happens." I just did exactly that when I wrote things like "they wriggle around," meaning that there is something (other than single pixels) that can become the subject of a sentence. Much better than nothing!

In fact, "pattern" is arguably the most general term we can use for something like this. I'll go even further: "pattern" is a close synonym of "predictability." What is predictable can be called a pattern, and whatever you call a pattern—whether it is a shape you're looking at, a sequence of related events, or something more abstract—is always grounded in your ability to foresee some aspects of it.

"Pattern," then, is the opposite of "random behavior." They don't exclude each other, though: you usually have patterns in the middle of randomness, just like the animation above. This is why people can make some predictions about notoriously random things like a stock market or an elementary particle—to the extent that someone can predict it, it is a pattern. The rest is random.

In other words, randomness and patterns are inversely proportional, as you can see by comparing the last universe with this new one. Here, I cranked the probability of "joining the majority" up from 60% to 90%, reducing the randomness.

Now the pixels form much more recognizable, stable blobs. They are more predictable because you can be quite confident that they'll maintain roughly the same general shape for at least a while.

Even though you can't predict the entire future of any given blob—predictability usually has a time horizon—you can now make educated guesses about what the color of any given pixel will be several frames ahead. The randomness has decreased, and the patterns have become proportionally stronger.

So strong, in fact, that you could give proper names to the cutest of those blobs. One that looks a bit like a worm you could call Mr. Wriggles, and another resembling a hat could be Professor Brimley. Go ahead, invite your friends over and place bets with them, pit your predictive powers against each other. Will Mr. Wriggles eventually devour old Prof. Brimley, or will Brimley cover Wriggles entirely?

Patterns are literally all we can talk about. Patterns are all we can think and care about. Let me rephrase that: no thought, no language, no notion of existence is possible without patterns of some kind.

II / Why?

This is interesting and all to ponder about, but it also raises some big questions.

First, why do new patterns form when you reduce randomness? All we did was make each pixel sometimes imitate its neighbors. Not a very sophisticated rule. It's not obvious why this would lead to the growth of nice, plump lumps behaving precisely like that, with those specific sizes and curves.

The answer is recursion. Adding that neighbor-mimicking behavior created the ability for each pixel to affect its own color at a later time. The fact that pixel A is green at Frame 1 will impact A's neighboring pixel's color at the next frame and may well push some of them to become green. This, in turn, means that those neighbors will impact the probability of A being green again two or more frames down the road. This is a case of recursion—a feedback loop—and it's the reason why you find some level of stability and predictability in those patterns.

In the fully-random example, on the other hand, each pixel was created entirely from scratch at every time step, regardless of what happened before. No recursion could happen then: no pixels affecting themselves over time, no reinforcement of previous colors, no patterns, no predictability.

The second question is why these patterns are predictable at all, and it has to do with another key property of causal links like the color-updating rule I introduced.

Although I only allowed a pixel to "remember" the color of its neighbors in the previous frame—and no earlier!—this unlocked something much grander: the neighbors in the previous frames also "remembered" their respective neighbors from two frames ago, those of two frames ago "remembered" their own neighbors from three frames ago, and so on in an uninterrupted chain. This enables what's technically called "history-dependence", the relationship between what's happening right now with everything that happened before, since the beginning of time.

History dependence is the secret sauce that lets you make predictions based on patterns: by knowing what those patterns did in the past, or elsewhere—stay still, wriggle around, disappear after a certain time, etc.—you can extrapolate predictions of what they might do in the future. Randomness, on the other hand, knows no history. (Turns out that it's very hard to have history-dependence without also triggering some kind of recursion, like in this case.)

But there is something even deeper and more counterintuitive to be gleaned from this simple universe: novel patterns can arise spontaneously out of pure, utter randomness. One moment there is nothing; the next moment you have Wriggles and Brimley squirming their ways around. Depending on the nature of the interactions, a field of "nothing in particular" can give rise to something that can be said to "exist" as its own thing. Meaningfulness born from meaninglessness. Order out of chaos.

III / Water Lilies

Although the pixels of the first simulation had the same probability of assuming any of the available colors, in the less-random cases this probability became "loaded" or skewed, with some colors more probable than others. At the level of the single pixel, in a single frame transition, this skew was intentionally designed by me in the form of my neighbor-mimicking rule. But recursion brought the skew much farther than I designed it. By reinforcing its skew over many frames, recursion made whole neighborhoods acquire the same color, so that the probability of those neighborhoods collectively retaining the same color became much higher than that of single pixels.

Echoing my earlier essay, something unlikely became likely thanks to the self-reinforcing work of recursion. The long-lived blotches of color bordering each other—very rare in the fully-random universe—became the norm. I call the outcomes of such probability-enhancing feedback loops Water Lilies.

Almost all patterns that exist in reality are Water Lilies: the results of feedback loops, often arising spontaneously from random origins.

Let's leave this pixel world now and return with our minds to our own vast Universe. To avoid confusion with the complexity of biology, let's imagine a barren, lifeless planet. Here, too, Water Lily patterns abound, thanks to myriad kinds of recursion.

The fact that the planet itself exists is a Water Lily, that is, a product of recursion: gravity first caused a small clump of dust and debris to accrete out of a randomly swirling primordial cloud; this clumping in turn caused the local pull of gravity to strengthen, pulling more clumps closer, and so on in a loop that swept up most of the nearby matter into a single dense object. This process created the pattern "celestial object," because its compactness means that it keeps existing predictably over a long period of time—just like the uniform neighborhoods in the simple universe.

The planet's spherical shape is a pattern, too, because you can predict or reconstruct its whole shape by looking only at a part of it. This highly non-random shape is another Water Lily, of course, because any random protrusion it had at the beginning was pulled down by gravity, increasing the internal pressure of the planet, and that internal pressure in turn pushed out the valleys that were too deep. A recursive cycle that can only end with a neat ball. In the pixel universe, the relatively smooth borders of the blobs were something analogous, although they were based on a different recursive rule.

The stratification of the planet's inner layers, another neat pattern, is a Water Lily, for reasons I explained elsewhere;

the conical shapes of the planet's volcanoes are Water Lilies, as are their roughly periodic (i.e., not-fully-random) eruptions;

the fact that rivers of lava and other liquids on the planet's slopes are able to "find" their ways to the lowest depressions in the ground is a Water Lily;

the tidal locking of a moon (like Earth's) that makes it always display the same face towards its planet is yet another Water Lily effect.

The list goes on. In short, nearly anything you can predict even a little—anything you can label with a name and describe in some way—emerges out of randomness with a (possibly very long) sequence of recursive interactions.

IV / Perspective

Despite all that, perhaps you still find it hard to believe that the Universe would have become so full of amazing and diverse patterns, all arising spontaneously from the random quantum noise of the Big Bang. If that is the case, try putting things in perspective.

According to rough back-of-the-envelope estimates, all solid, concentrated matter in existence occupies a total volume of space equivalent to one part in 3,200,000,000,000,000,000,000,000,000,000,000,000,000,000 of the Universe's volume. To give you a sense of the scale, if the Universe were a bag as large as the Earth, all structured matter inside it would be 15 times smaller than a single virus—let's say the leg of a virus.

That virus leg accounts for nearly all patterns humanity knows and talks about, from stars and planets to all living creatures, places, and objects, scattered in that Earth-sized bag.

Everything other than all patterns is empty space, peppered with largely un-pattern-like things like gas and dust clouds, stray particles zipping around, and dark matter. But these things are so poor in patterns that there is very little we can say about them—despite the fact that they comprise an enormous, crushing majority of the Universe's volume. And so we tend to ignore them altogether.

Patterns are not that common, after all. Recursion is what makes improbable things like planets and worms probable, sure, but it does so quite rarely. We just happen to be in the midst of it all. ●