There is a lot of talk, nowadays, about mental models and thinking frameworks, yet these concepts are both vastly underrated and poorly understood. Here I want to make the claim that they are (*ominous gongs*) the very foundations of all human thought, and that it is worth understanding them in full. My definitions of the terms might be slightly different from others you've seen before (there aren't universally accepted definitions to begin with), but hopefully the explanations and examples below will make them crystal clear.

Models

A model is an analogy. It is a simplified simulation of something else. Systems mimicking other systems. Models are intuitive, at least when they are physical and tangible. We all see them around us every day: a map is a model of a place, a photograph is a model of a scene, and an architect's model is, well, a model of a building. A model doesn't have to resemble the thing it models, though. For instance, even a thermometer is a model, because it approximately replicates a range of variation that helps you know what to expect (e.g. the sense of being hot or cold, based on the temperature).

Typically—although not always, and not for everyone—we are familiar with the limitations of models, stemming from the simplifications they always entail. A map can be inaccurate, outdated, and limited in scope; a photograph doesn't fully convey what was going on when it was shot; and an architectural model usually looks way cleaner and neater than the final product (architects, those sneaky foxes). In the famous words of Alfred Korzybski, the map is not the territory, and the word is not the thing. No matter how sophisticated the analogy, it is never the same as the thing it refers to.

We use models in our minds too, although those tend to be more abstract and less intuitive. You may have heard of Occam's Razor—the simplest explanation is usually the best one—referred to as a mental model, but what does it simulate? The answer must be, "it simulates someone making a correct judgement", which is why it is useful as a rule of thumb. Clearly it is a simplification, because sometimes there are special reasons for the simplest explanation to be wrong, but (according to William of Occam) it is right most of the time.

Other mental models popular on the internet are even fancier, with catchy names like Hanlon's Razor, Eisenhower Matrix, and Pareto Principle. But most of the models we use don't have a name—in fact, we build new ones up all the time. Don't let bloggers and self-help gurus convince you that "Using Mental Models is What the Smart Kids Do", because it is impossible to think without mental models, regardless of one's IQ. Everybody is forced to use them every second of their lives, because we live by predicting the future, and mental models is how we do that. Simulating the world is what our brains are (largely) for. Some examples below should make this point clearer.

Framings

Framings are less intuitive. They, too, are mentioned sometimes in relation to how we think, together with the related and often overlapping terms "frames of thought", "thinking frameworks", and "schemata". They seem to involve seeing things in different lights, and interpreting events and situations in a positive or negative way. Yet the meaning of these words is slippery and elusive, and their relationship with mental models unclear.

That's a pity, because it's a very useful concept. So here is a plain definition: a framing is a choice of boundaries. Reality is a continuum, with no neat inherent separation or boundaries between things, because everything affects, and is affected, by everything else around. It is up to us sentient beings to invent boundaries so that we have something to build our mental models with.

Is the hand a separate entity from the arm it is attached to?

Are the people born in this city compatriots of those born in that other city?

Where exactly does the atmosphere end and space begin?

Is light the absence of darkness, or the other way around?

How many basic human rights are there?

None of these questions makes any sense from a physical point of view, and Nature offers no hints. But the moment people are involved, those questions could begin to matter. We often find that we must answer them one way or another, even if arbitrarily, just to understand each other and get along with our lives. Whenever we define a word, we're making a framing.

But a framing is also a choice of what exists and what doesn't—what's inside and outside of an ontological boundary. The possible ways to frame reality are virtually infinite, but our time and mental capacities are finite. Like a child choosing which dolls or toy bricks to play with at the beginning of playtime, we must choose what counts as "a thing" and what can be waved away as irrelevant. This cherry-picking work also includes any salient or meaningless details about what's inside the things we take to exist.

Only after we have defined our moving parts like that, can we begin to think about what those things do, i.e. we can simulate the world with our models.

Thus every model needs a framing. In other words, given that we use models for everything, framings are an equally central concept for cognition. In short:

A framing is a set of black boxes, and it answers the question: what exists in the first place, and what properties does each of those things have?

A model is a prophesy device, and it answers the question: what happens when those things that exist interact? What do those black boxes do together?

Six Examples

Armed with these two definitions, let's look at some examples in order of increasing familiarity.

Example 1: Bohr's Model of the Atom

Science is where the use of models is most explicit and deliberate. The word "model" itself it used most often by scientists, and it refers to the condensation of centuries of study into powerful prediction tools.

Take, for instance, the Bohr model of the structure of the atom, also known as the "solar system model". In the late 1910's, the physicist Niels Bohr chose a framing approximately as follows:

• There exists a phenomenon called electromagnetic force with certain properties.
• There exist particles called nuclei with positive charge.
• There exist negatively charged particles called electrons, and they can only have energies in discrete amounts, i.e. quantized.

These were his black boxes. It wasn't clear at his time what the nuclei were made of, nor that those particles also had a wave-like nature (that would come a few years later with de Broglie, Schrödinger, and the rise of quantum mechanics). But Bohr had access to a lot of knowledge about the behavior of electrons and of atoms, and to many well-known physical theories like electromagnetism and all of classical mechanics. With these assumptions, he put forth a model for how those particle black boxes might work together:

The electrons settle in orbits around the nucleus; due to the quantization of their energy, these orbits exist at distances that are discrete multiples of a base distance (which he computed); plus more details that we'll gloss over.

This model worked better than its predecessors, because it made more accurate predictions, like the energy levels and the spectral lines of hydrogen atoms. In this sense, it was a "good" model. Although it was replaced only a few years later by much more powerful models from quantum physics, it served as a stepping stone to better understand those natural phenomena. (Its simplicity was perhaps a bit too effective, because we still tend to think about and represent atoms as little solar systems, despite the fact that we've long since discovered they don't look like that.)

Example 2: Supply and Demand

One of the most fundamental models in macroeconomics is the law of supply and demand. Its framing goes something like this:

• There exists something being traded, called a good.
• There exists a value, called price, for which the good can be sold.
• There exists a perfectly competitive market, i.e. a large group of buyers and sellers of the same good with no barriers to their trade, nor special advantages or disadvantages given to anyone.
• There exists something called supply, meaning the amount of the good for sale in the market; this supply decreases or increases as the price goes up or down.
• There exists something called demand, the amount of the good that people are seeking to buy in the market, which grows as the price goes down and vice versa.

Again, these are black boxes, because it doesn't matter how many people there are in the market, why they want to buy the good, or what the good even is. With these, the model is simple:

The price, supply, and demand will change until they reach the point where supply and demand are identical.

This model is thousands of years old and it is here to stay, because it works. But it doesn't work nearly as well as we typically need. Its extreme simplicity makes it memorable and easily applicable, but it ignores too many factors to be truly realistic. To increase its accuracy (somewhat), economists have had to expand the framing to include many more factors, like:

• Forms of imperfect competition, like monopolies and oligopolies
• Innovation and entrepreneurial disruption
• Asymmetric information, with some traders much more well-informed than others
• And many more.

With more moving parts, the model becomes exponentially more complex—a common trade-off for models.

Example 3: Weight Loss

Of course, models are not confined to the blackboards of professors and analysts. An example of a model we often apply in daily life is the basic formula for weight loss.

First, the framing:

• There exists a type of organic mass called fat, which is generally considered unhealthy and unattractive if you have more than a certain amount of it.
• There exists an activity called exercise, which you can do by dedicating money, time, and sweat.
• There exists another activity called a diet, which is the quantity and quality of food you eat.

The model is this:

Exercising more and following a better diet leads to a decrease in fat.

This model is a benefic one, because it motivates people to follow a healthier lifestyle, even though it is extremely rough (there are countless theories about what a "better" diet looks like, which makes all the difference) and grossly inaccurate (exercise is great for health but very ineffective for weight loss). We tend to think in these terms, and when we decide to start a Paleo diet or to sign up to a gym, we're—more or less implicitly—using this model.

Example 4: Favorite Creators

Take a famous creator you're a fan of, like a pop star or a writer. For the sake of this example, I'll use the American filmmaker Wes Anderson.

The framing:

• There exists a medium of exchange of abstract value called money.
• There exists a property of reality which separates events in a continuum, called time.
• There exists this human being called Wes Anderson who makes movies (and also breathes and eats, I guess).

That's all we need in the framing. We don't need to assume that a place called Hollywood—or even the idea of "space"—exists, we don't need to know anything else about Wes. We can go straight ahead with the mental model:

If someone gives Wes $25 million and a couple of years (and this happens regularly), he'll release an amazing movie.

A film producer who is asked to produce Wes's next film might need a more extensive framing (what is Wes's next idea, which actors are available, where the film should be shot, etc.) and a more sophisticated model for how those additional black boxes might work together, but for me, the above is an accurate-enough prophesy device, and it has never fully failed me over the years.

Example 5: Kicking

During a sports match, there may come a time when you are called upon to kick a ball and to kick it well.

You're using a framing and a model here, too, although in this case they are more automatic and non-verbal. The framing would probably involve certain specific movements of your legs that you've learned to make, the position and speed of the ball, and the targets you wish to deliver the ball to. The model is your mental expectation of where the ball will go if you kick it in this or that way, with this or that timing.

If you're a beginner, your framing will be barebones: you can only focus on a few things at once, perhaps only the ball's location, with no time to consider anything else. As you practice your kicks, you learn to take more factors into account, like the assigned and actual positions of your team mates and opponents, and your mental simulation grows in accuracy and confidence.

If you've ever worked hard at a sport, you probably know the feeling of suddenly discovering a subtly different way to use your body, one that you could have used any time before if only it had occurred to you. That discovery is you expanding your framing of the task. But in order to master that new technique, you'll need to refine your mental model (and muscles) through practice.

Example 6: Going Meta

Clearly, the act of saying "there are framings and there are models" is itself a new framing (a meta-framing?). By writing all these words to explain what these two concepts imply and how they can help you think more clearly, I'm laying out the model that I built with them. (A discussion of framings about framings about framings will have to wait for another blog post.)

The Crux of Framings

Here is the issue: much more so than mental models, our use of framings is almost always unconscious and implicit. We don't usually sit down in front of a Framing Catalog and say, "let me make a prediction based on... hang on... yep, this framing should do the job!"

We find it easy to speak about our models and we often argue about which predictions we believe to be more accurate—what could happen, how the world works, etc. But we rarely question our framings. We seldom take a step back to ask what other factors might be at play, and if the definitions of our words are really solid and compatible with other people's. This might be fine for semi-automatic activities like muscular movement and day-to-day tasks with low stakes, but it's a big mistake whenever serious thought is involved.

Forgetting that framings are at the root of all our thinking leads to being oblivious that those assumptions we're making about the world are somewhat (or entirely) arbitrary and ad hoc. We miss the opportunity to seek other fruitful ways to segment the world in order to solve any given problem.

What's worse, relying on unconscious framings also means that we suffer from massive blind spots, because we forget that we're hand-waving away most of reality in order to have neat, workable models. I like to call the latter issue tunnel vision: we get so entrenched in our little framings that we start to believe that they are the whole of reality, often with depressing consequences. (More on this in future blog posts.)

The Art of Boundarycraft

Suppose you do remember that your framings are tools at your disposal, how can you optimize them? Well, besides replacing them altogether with others, there are only two logical approaches: you can change the resolution, and you can move the boundaries.

By "changing the resolution of your framing", I mean either clumping things together into bigger black boxes to make a more general framing, or trying to figure out what's going on inside your current black boxes, effectively increasing the number of moving parts that you can simulate in your models. We could also call these two operations zooming out and zooming in.

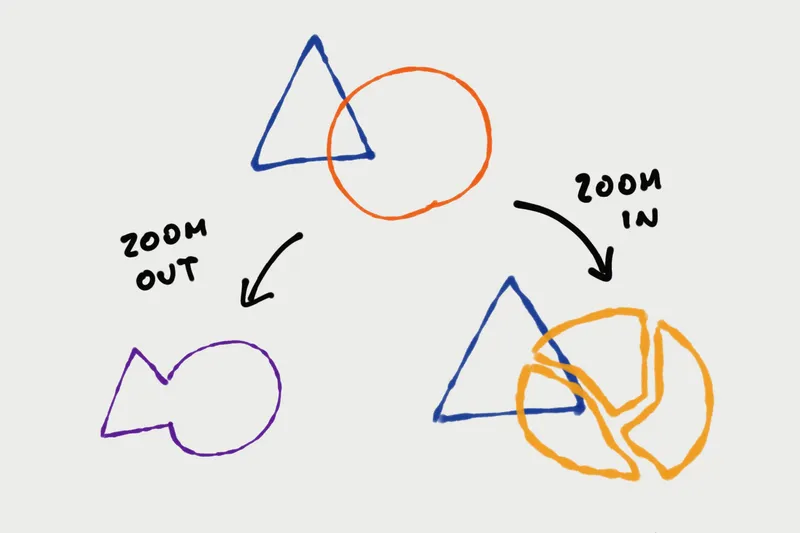
Zooming out—decreasing the resolution of your framings—is what philosophers do when they try to come up with universal categories and overarching explanations for reality or the human condition. It is also what theoretical physicists do when they chase "grand unifying theories", a few simple formulae capable of explaining (simulating) as many different phenomena as possible.

The risk and trade-offs of over-simplification remain, but when you carefully zoom out your framings, you're learning to notice patterns in the world that you had been oblivious to before. The details fade away, things seem simpler and more regular. Perhaps this is what it means to become wiser.

Zooming in, on the other hand, is about reverse-engineering reality. It's asking questions about why things work in a certain way, instead of being satisfied with knowing they do. Again, this is something scientists do systematically: observe deviations from our predictions, take into account smaller and subtler factors, build hypothetical models for how those factors could interact, and experiments to validate those models. For example, when quarks were discovered, what used to be a "nucleon" black box (proton or neutron) was replaced with a model composed of three smaller "quark" black boxes.

Science is a bunch of good-enough framings and the best models we can devise on top of them. At the individual level, a higher-resolution model means being not only more knowledgeable, but also better at predicting what the system at hand can or will do—it means being smarter. Of course, you could do it the scientist's way, or you could open a book or attend a lecture and have other people teach you those higher-resolution framings.

The second thing you can do with your malleable framings is to "move the boundaries". This doesn't necessarily imply any kind of zooming, but it is more cataclysmic in nature. You're metaphorically redrawing the map, and this could lead to new continents emerging from the waters, old borders being shifted, and land bridges appearing across straits.

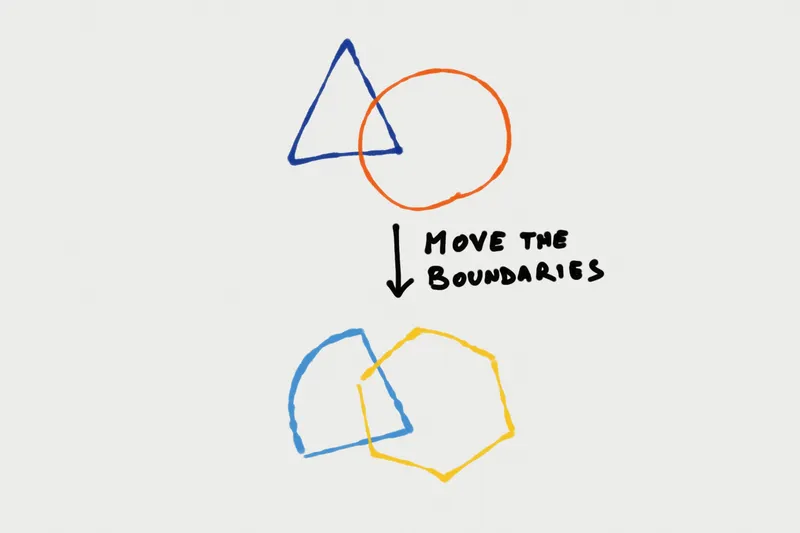
Moving the boundaries is what the pioneers of quantum mechanics did in the 1920's, when they decided that being a particle and being a wave were not mutually-exclusive descriptions. It's what avant garde novelists like James Joyce did in the early 20th century, when they expanded the reach of the occasional description of a character's thoughts to fill whole books in the form of a "stream of consciousness".

You're moving the boundaries when you realize that exercise is important for your fitness but not for your body weight, or when you learn (like I did) that the way you experience the world is only one variation out of many. Shifting a framing's boundaries is what we mean with the term "thinking outside the box".

Changing the resolution of our framings is an excellent way to refine our understanding and predictions of the world, and people do at least some of that regularly in schools (mainly zooming in) and in universities (zooming both in and out). But it is by moving the boundaries that we can make the biggest leaps—what philosophers call "paradigm shifts". And you can only move a boundary if you're well aware that it exists in the first place. This is why we need to be thinking about framings even harder than we think about models.

The best and surest way to learn that art is to be somewhat versed in the scientific method. Science is humanity's mistake-minimizing tool, and in this sense it is very much not a prerogative of PhDs and "rational people": the methods at its core are essential to the day-to-day thinking of every human being, whatever their intellectual inclinations and interests. That is not to say that scientists are all masters of the art of framing and reframing: in my experience, they very often are not. Even they can benefit from the acquired habit of putting their models to rest for a while, taking a step back, and revisiting their base assumptions. A new good paradigm might be just a boundary-tweak away. ●

Other AeMu posts about these topics:

• Embedded Prophesy Devices
• Internal Model Translation Table
• Boundaries Are in the Eye of the Beholder
• A Framing Is a Choice of Boundaries
• A Fundamental Framing of Human Language
• "Bad" Framings
• A Black-Box View of Life
• Philosophy Is the Battle Against the Bad Framing Kraken